Kumpulan Soal Sifat Sifat Determinan Matriks
Apabila semua elemen dari salah satu baris atau kolom sama dengan nol maka determinan matriks tersebut adalah nol. Yang mana ada yang dapat dilakukan untuk menghitung dan menentukan determinan pada sebuah metriks berordo 33 ini yakni seperti berikut.
Yang kedua menggunakan Metode Minor-Kofaktor.

Kumpulan soal sifat sifat determinan matriks. Ada beberapa sifat sifat determinan matriks yaitu diantarannya. B bisa lebih dari dua A B C dst A n A n A-1. Desember 2 2020.
Mengenal pengertian ordo matriks menentukan determinan suatu matriks menentukan nilai x yang memenuhi persamaan matriks dan konsep kesamaan matriks. Apabila semua elemen dari salah satu baris atau kolom sama dengan nol maka determinan matriks tersebut adalah nol. Yang pertama adalah menggunakan Metode Sarrus.
Karena baris garis horisontal dalam matriks yang diperbesar beresuaian dengan persamaan dalam sistem yang diasosiasikan dengan baris tersebut maka ketiga operasi ini bersesuaian dengan operasi berikut pada baris matriks yang diperbesar. Sifat sifat determinan matriks inilah yang nantinya dapat dijadikan pedoman dalam menyelesaikan soal soal yang tersedia. 4a b 4a - 4b Pembahasan.
Misalkan matriks a memiliki ordo 3 x 4 dan matriks b memiliki ordo 4 x 2 maka matriks c memiliki ordo 3 x 2. Jika matriks A diketahui seperti di bawah ini maka determinan A adalah. Seperti matriks dengan elemen nol matriks segitiga atasbawah dan matriks dengan baris sebanding.
Cara Mudah Menyelesaikan Determinan. 4a 4b a -b C. Agar lebih mengerti perhatikan contoh soal.
Ab t b t a t. Sifat sifat determinan dari matriks. Kumpulan soal mudah sedang sukar.
76 soal dan pembahasan operasi matriks terbaru. Soal yang telah kami rangkum ini sering keluar dalam ulangan ataupun ujian nasional jadi. B A.
Sifat Sifat Determinan Matriks Ada beberapa sifat sifat determinan matriks yaitu diantarannya. Contoh soal dan jawaban determinan matriks 2 2. Metode ini dapat diterapkan untuk semua nxn matriks.
A b 4a - b B. Pembahasan soal umpn 2018 bidang rekayasa kode soal 33. A t A A.
Banyak rumor yang mengatakan bahwa matriks merupakan materi matematika yang paling gampang dipahami di tingkat sma. Sifat Determinan Matriks Ada beberapa sifat pada determinan matriks diantaranya yaitu. P dan q adalah matriks 2 2 seperti yang terlihat di bawah.
Bila semua elemen dari salah satu kolom sama dengan nol maka determinan matriks tersebut adalah nol. Sifat Sifat Determinan Matriks Determinan matriks memiliki sifat sebagai berikut. Untuk itu determinan matriksnya dapat.
Jadi penting bagi teman-teman untuk menguasai sifat-sifat determinan dan invers matriks. Metode OBE 4x4 Metode Sarrus 4x4 Metode Kofaktor 4x4 Metode OBE Pdf yang dibahas kali ini berkaitan dengan eliminasi Gauss sifat-sifat determinan dan matriks segitiga. A 1 1 A adjoint A Contoh soal 7.
Terimakasih smeoga ilmu yang baru saja di dapat bisa bermanfaat dan berguna. Matriks - Perkalian Determinan Invers Rumus Contoh Soal. Beberapa sifat matriks adalah sebagai berikut.
Contoh soal jawaban determinan matriks. 4a 4b 4a - 2b E. Untuk soal-soal seleksi masuk perguruan tinggi banyak sekali soal-soal matriks harus kita selesaikan dengan sifat-sifatnya.
Jika A a b c d maka A 1 1 ad bc d b c a Matriks d b c a disebut dengan matriks adjoint A ad bc adalah determinan matriks A sehingga. Contoh Soal Matriks Determinan dan Invers Pilihan Ganda dan Kunci Jawaban beserta Pembahasan Bank contoh Soal Matriks Determinan dan Invers matriks lengkap dengan Jawaban beserta Penyelesaiannya untuk Siswa yang berjumlah 20 butir. Matriks pada umumnya dapat dibagi menjadi beberapa macam tergantung besar ordonya.
Sifat-sifat determinan matriks sangat bermanfaat ketika menghitung matriks-matriks dengan karakteristik khusus. Tiga cara menghitung determinan matriks 4x4 yaitu. Pada pemabahasan sebelumnya kita telah mengdiskusikan bagaimana mencari determinan suatu matriks baik matriks yang berordo 22 maupun matriks yang.
Seperti pada contoh berikut ini. Invers matriks A berordo 2 x 2 adalah adjoin dari matriks A dibagi dengan determinan matriks A. Soal Ketiga Determinan Matriks Ordo 3 3.
Rumuscoid Makalah materi definisi pengertian sifa-sifat rumus dan contoh soal determinan matriks ordo 22 ordo 33 ordo nxn dimana pada kesempatan sebelumnya kita juga telah membahas tentang invers matriks. Soal dan jawaban ujian materi matriks. Perhatikanlah soal latihan berikut ini.
Det A 4a 2 - 4b 2 4 a 2 - b 2 det A 4 a b a - b. Menjelaskan kembali cara menentukan determinan dan invers matriks dengan memahami elemen diagonal utama elemen diagonal samping dan adjoin matriks. 4a 2b 4a b D.
Sifat determinan ini berlaku untuk semua ordo matriks persegi yaitu matriks 22 33 44 dan seterusnya.

Determinan Matriks Pengertian Sifat Sifat Dan Contoh Soal

Determinan Matriks Ordo 3 X 3 Simpel Mudah Enteng Ndak Bikin Pusing Samasaya Belajardirumah Youtube

Kumpulan Soal Dan Pembahasan Determinan Matriks Mata Pelajaran

Determinan Dan Invers Matriks Ordo 2 Matematika Sbmptn Un Sma Youtube

37 Determinan Matriks Berordo 5x5 Dengan Metode Ekspansi Kofaktor Youtube

Determinan Matriks Pengertian Sifat Dan Contoh Soalnya Lengkap Tutorialbahasainggris Co Id

Determinan Matriks Q Materi Determinan Q Contoh Soal

Soal Asli Utbk 2019 Matematika Saintek Determinan Matriks Youtube Matematika Pengetahuan Asli

Contoh Soal Dan Rumus Matriks Invers 2x2 3x3 4x4 Lengkap
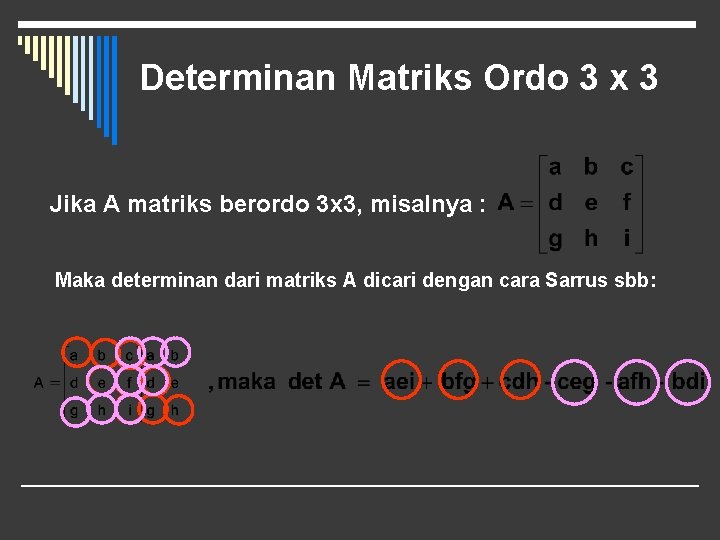
Determinan Matriks Q Materi Determinan Q Contoh Soal

15 Contoh Soal Determinan Dari Matriks Kumpulan Contoh Soal

Determinan Matriks Q Materi Determinan Q Contoh Soal

Cara Mencari Determinan Dan Invers Matriks Matematika Kelas 11

Contoh Soal Dan Jawaban Determinan Matriks 2 2 Bali Teacher
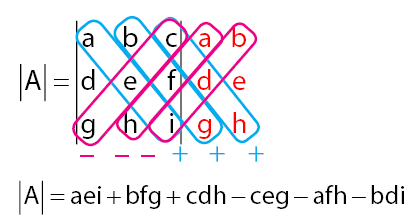
Determinan Matriks Invers Matriks Sifat Sifatnya Idschool

Determinan Matriks Ordo 3 3 Ppt Download

Contoh Soal Matriks 3x3 Dan Pembahasannya Download File Guru
24 Contoh Soal Determinan Matriks Mencari Nilai X Kumpulan Contoh Soal
.png?width=437&name=penyelesaian%20invers%20matriks%203x3%20(1).png)
Cara Mencari Determinan Dan Invers Matriks Matematika Kelas 11


Posting Komentar untuk "Kumpulan Soal Sifat Sifat Determinan Matriks"